ਬਹੁਤ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਪੜ੍ਹਨ, ਸਮਝਣ ਅਤੇ ਤੁਲਨਾ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਤੇ ਕਿਰਿਆਵਾਂ ਕਰਨ ਵਿਚ ਮੁਸ਼ਕਿਲ ਹੁੰਦੀ ਹੈ।

ਬਹੁਤ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਪੜ੍ਹਨ, ਸਮਝਣ ਅਤੇ ਤੁਲਨਾ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਤੇ ਕਿਰਿਆਵਾਂ ਕਰਨ ਵਿਚ ਮੁਸ਼ਕਿਲ ਹੁੰਦੀ ਹੈ। ਅਕਸਰ ਸਾਨੂੰ ਬਹੁਤ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ। ਉਦਾਹਰਣ ਦੇ ਤੌਰ ’ਤੇ ਬ੍ਰਹਿਮੰਡ ਦੀ ਉਮਰ ਸਾਲਾਂ ਵਿਚ, ਧਰਤੀ ਦਾ ਪੁੰਜ ਟਨਾਂ ਵਿਚ, ਸੂਰਜ ਦੀ ਧਰਤੀ ਤੋਂ ਦੂਰੀ ਕਿਲੋਮੀਟਰਾਂ ਵਿਚ ਆਦਿ ਕੁੱਝ ਅਜਿਹੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ ਜੋ ਬਹੁਤ ਵੱਡੀਆਂ ਹਨ। ਏਨੀਆਂ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਆਮ ਤੌਰ ’ਤੇ ਸ਼ੁੱਧ ਨਾ ਹੋ ਕੇ ਲਗਭਗ ਹੁੰਦੀਆਂ ਹਨ।

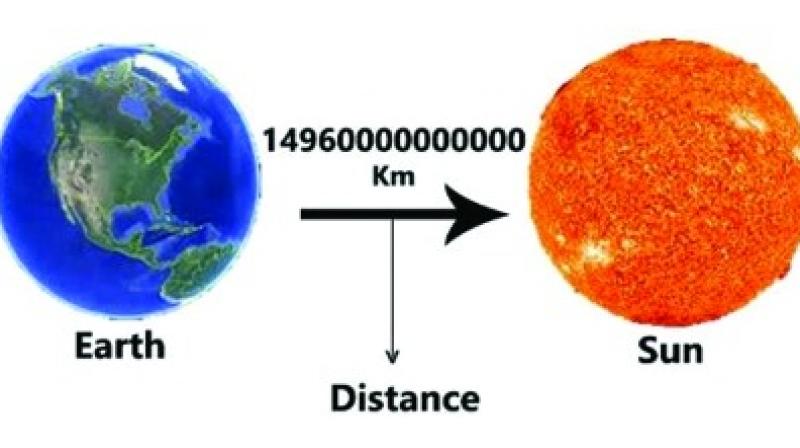
ਉਦਾਹਰਣ ਦੇ ਤੌਰ ’ਤੇ ਖ਼ਲਾਅ ਵਿਚ ਪ੍ਰਕਾਸ਼ ਦਾ ਵੇਗ 299792.5 ਕਿਲੋਮੀਟਰ ਪ੍ਰਤੀ ਸੈਕਿੰਡ ਹੁੰਦਾ ਹੈ, ਪਰ ਵਰਤੋਂ ਵਿਚ ਇਸ ਦਾ ਮਾਨ 300000 ਕਿਲੋਮੀਟਰ ਪ੍ਰਤੀ ਸੈਕਿੰਡ ਜਾਂ 300000000 ਮੀਟਰ ਪ੍ਰਤੀ ਸੈਕਿੰਡ ਲੈਂਦੇ ਹਾਂ। ਇਸੇ ਤਰ੍ਹਾਂ ਬ੍ਰਹਿਮੰਡ ਦੀ ਉਮਰ ਲਗਭਗ 8,000,000,000 ਸਾਲ ਹੈ। ਸੂਰਜ ਦੀ ਧਰਤੀ ਤੋਂ ਲਗਭਗ ਦੂਰੀ 150,000,000 ਕਿਲੋਮੀਟਰ ਹੈ। ਧਰਤੀ ਦਾ ਪੁੰਜ ਲਗਭਗ  5980,000,000,000,000,000,000 ਮੀਟ੍ਰਿਕ ਟਨ ਹੈ। ਇਹਨਾਂ ਸੰਖਿਆਵਾਂ ਵਿਚ ਜ਼ੀਰੋਆਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਗਈ ਹੈ। ਦਿਲਚਸਪ ਗੱਲ ਇਹ ਹੈ ਕਿ ਭਾਰਤ ਵਿਚ ਹੀ ਇਹ ਇਕ ਨਵੀਂ ਸੰਖਿਆ ਜ਼ੀਰੋ ਅਰਥਾਤ ਸਿਫ਼ਰ ਦਾ ਜਨਮ ਹੋਇਆ ਸੀ। ਭਾਰਤ ਨੂੰ ਇਸ ਲਈ ਹੀ ਗਣਿਤ ਦਾ ਵਿਸ਼ਵ ਗੁਰੂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।

ਏਨੀਆਂ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਭਾਵੇਂ ਅਸੀਂ ਜ਼ੀਰੋਆਂ ਲਗਾ ਕੇ ਲਿਖ ਸਕਦੇ ਹਾਂ। ਪਰ ਪੜ੍ਹਨ ਜਾਂ ਲਿਖਣ ਸਮੇਂ ਮੁਸ਼ਕਲ ਜ਼ਰੂਰ ਆਉਂਦੀ ਹੈ। ਇਸ ਲਈ ਏਨੀਆਂ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਲਿਖਣ ਲਈ ਆਮ ਤੌਰ ’ਤੇ 10 ਦੀ ਘਾਤ ਅੰਕਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਸੰਖਿਆ 500,000,000 ਨੂੰ 5]108 ਜਾਂ 500]106 ਦੇ ਰੂਪ ਵਿਚ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਸਾਰੀਆਂ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ 10 ਦੀ ਘਾਤ ਅੰਕ ਦੇ ਰੂਪ ਵਿਚ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਸੰਖਿਆ 500,000,000 ਨੂੰ ਇਸ ਵਿਚ ਲਿਖਣ ਲਈ ਅਸੀਂ ਅਗਲੀ ਰਕਮ 5 ਅਤੇ 10 ਦਾ ਘਾਤ ਅੰਕ 8 ਜਾਂ ਅਗਲੀ ਰਕਮ 50 ਅਤੇ 10 ਦੀ ਘਾਤ ਅੰਕ 7 ਲੈ ਸਕਦੇ ਹਾਂ। ਪਰ ਇਸ ਸੰਕੇਤ ਪਧਤੀ ਨੂੰ ਅਸੀਂ ਹਮੇਸ਼ਾ ਵਿਗਿਆਨਕ ਸੰਕੇਤਕ ਜਾਂ ਸੰਖੇਪ ਰੂਪ ਵਿਚ ਲਿਖਦੇ ਹੈ।

ਇਸ ਵਿਚ ਅਸੀਂ ਮੁਢਲੀ ਸੰਖਿਆ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਚੁਣਦੇ ਹਾਂ ਕਿ ਇਹ 1 ਤੋਂ ਵੱਡੀ ਅਤੇ 10 ਤੋਂ  ਛੋਟੀ ਹੋਵੇ ਅਤੇ ਪਿੱਛੇ 10 ਦੀ ਘਾਤ ਇਸ ਦੇ ਰਹਿੰਦੇ ਅੰਕਾਂ ਅਨੁਸਾਰ ਚੁਣਦੇ ਹਾਂ। ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਪ੍ਰਕਾਸ਼ ਦੇ ਵੇਗ ਨੂੰ 3]108 ਮੀਟਰ/ਸੈਕਿੰਡ, ਬ੍ਰਹਿਮੰਡ ਦੀ ਉਮਰ 8]109 ਸਾਲ, ਸੂਰਜ ਦੀ ਧਰਤੀ ਤੋਂ ਦੂਰੀ 1.5]108 ਕਿਲੋਮੀਟਰ, ਧਰਤੀ ਦਾ ਪੁੰਜ 5.98]1021 ਮੀਟ੍ਰਿਕ ਟਨ ਜਾਂ 5.98]1024 ਕਿਲੋਗ੍ਰਾਮ ਲਿਖਾਂਗੇ। ਆਧਾਰ 10 ਦੀਆ ਘਾਤਾਂ ਦੀ ਤੁਲਨਾ ਕਰਨ ਤੇ ਸਾਫ਼ ਪਤਾ ਚਲਦਾ ਹੈ। 

2.7 ‘‘1012 ਹ 1.5” 108
ਜਿਸ ਤਰ੍ਹਾਂ ਘਾਤੀ ਸੰਕੇਤਨ ਬਹੁਤ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਦਰਸਾਉਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ, ਉਸੇ ਤਰ੍ਹਾਂ ਬਹੁਤ ਛੋਟੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਵੀ ਘਾਤ ਅੰਕੀ ਸੰਕੇਤਨ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਪਰ ਇੱਥੇ 10 ਦੀ ਘਾਤ ਦਾ ਮੁੱਲ ਰਿਣਾਤਮਕ ਅਰਥਾਤ ਘਟਾਅ ਵਿਚ ਹੁੰਦਾ ਹੈ। ਜਿਵੇਂ ਤਰੰਗ ਲੰਬਾਈ  ਦੀ ਇਕਾਈ ਏਂਗਸਟਰਾਮ ਹੈ ਅਤੇ ਇਕ ਏਂਗਸਟਰਾਮ ਦਾ ਮੁੱਲ 1/10,000,000,000 ਮੀਟਰ ਹੈ। ਇਸ ਸੰਖਿਆ ਨੂੰ ਅਸੀਂ 1” 10-10 ਮੀ. ਲਿਖ ਸਕਦੇ ਹਾਂ। ਇਸੇ ਤਰ੍ਹਾਂ ਸੰਖਿਆ 0.00000487 ਨੂੰ 4.87 ]10-6 ਮੀਟਰ ਲਿਖ ਸਕਦੇ ਹਾਂ।

ਹੁਣ ਅਸੀਂ ਸਾਰੀਆਂ ਵੱਡੀਆਂ ਅਤੇ ਛੋਟੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਵਿਗਿਆਨਕ ਸੰਕੇਤਨ ਜਾਂ ਸੰਖੇਪ ਰੂਪ ਵਿਚ ਸੰਖਿਆ ਦਾ ਮੁੱਲ 1 ਤੋਂ10 ਵਿਚਕਾਰ ਲੈਂਦੇ ਹੋਏ ਹੀ ਲਿਖ ਜਾਂ ਪੜ੍ਹ ਸਕਦੇ ਹਾਂ।

- ਸ.ਹ. ਸਕੂਲ ਇੰਦਰਗੜ੍ਹ, ਮੋਗਾ।
ਮੋਬਾਈਲ : 88725-26500